链表算法 I

今天 LeetCode 的每日一题是 142. 环形链表 II，最优解好神奇。看了 视频讲解 才搞懂，整理下作为笔记。

视频中讲解了如下几个算法：

1. 计算链表的中间节点
2. 是否是环形链表
3. 查找环形链表的入口节点
4. 重排链表

与本题相关的是 1 ~ 3，算法也比较类似。

1. 计算链表的中间节点

算法：

1. 定义两个指针 slow 和 fast 指向 head ；
2. slow 每次向后走一步，fast 每次向后走两步；
3. 直到 fast 是最后一个节点或最后一个节点之后的 null 时，此时 slow 节点即是中间节点。

说明：

1. 奇数个节点的场景

   
   

   

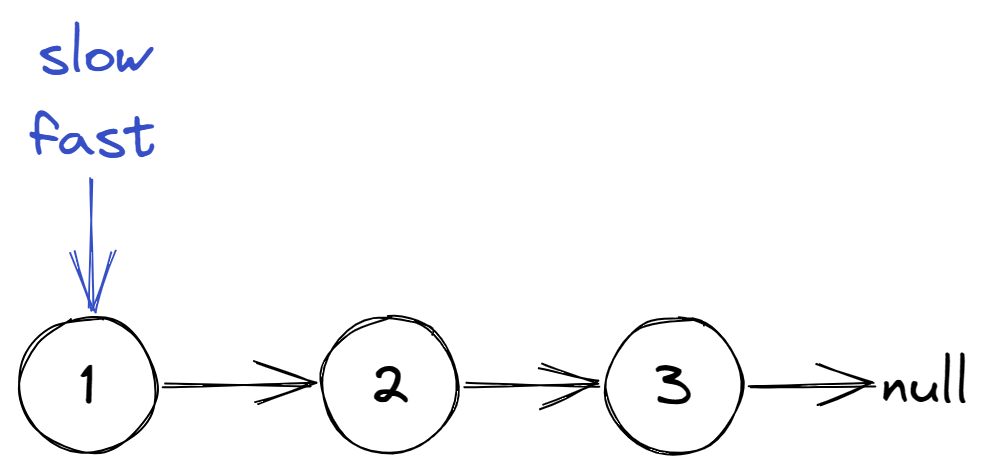
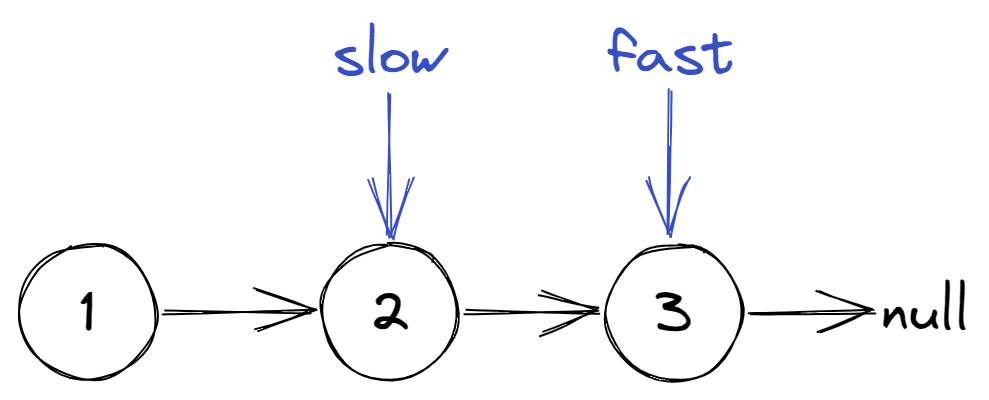
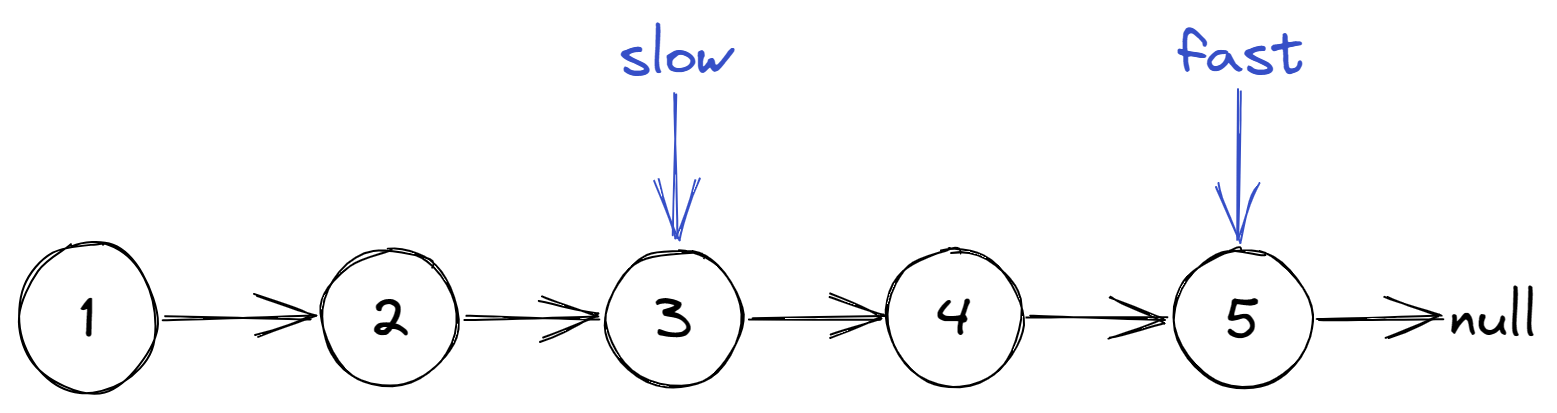
2. 偶数个节点的场景

   
   

   

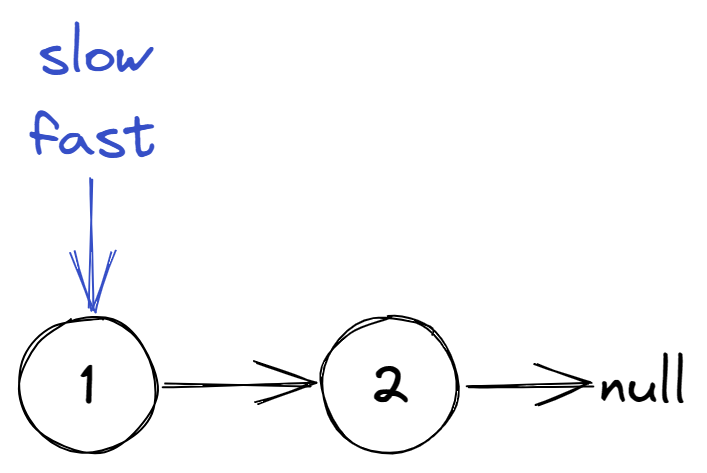
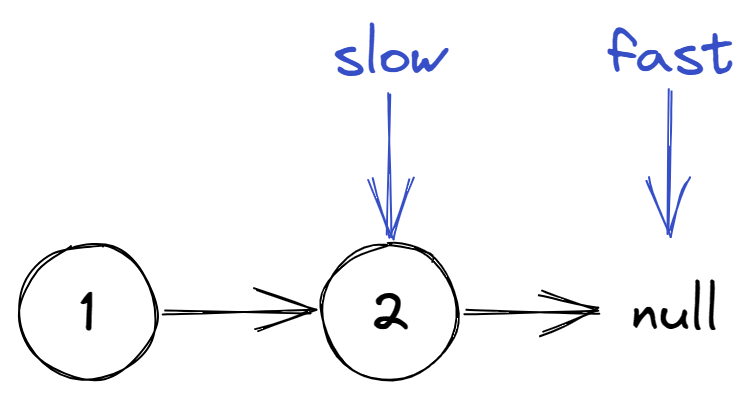
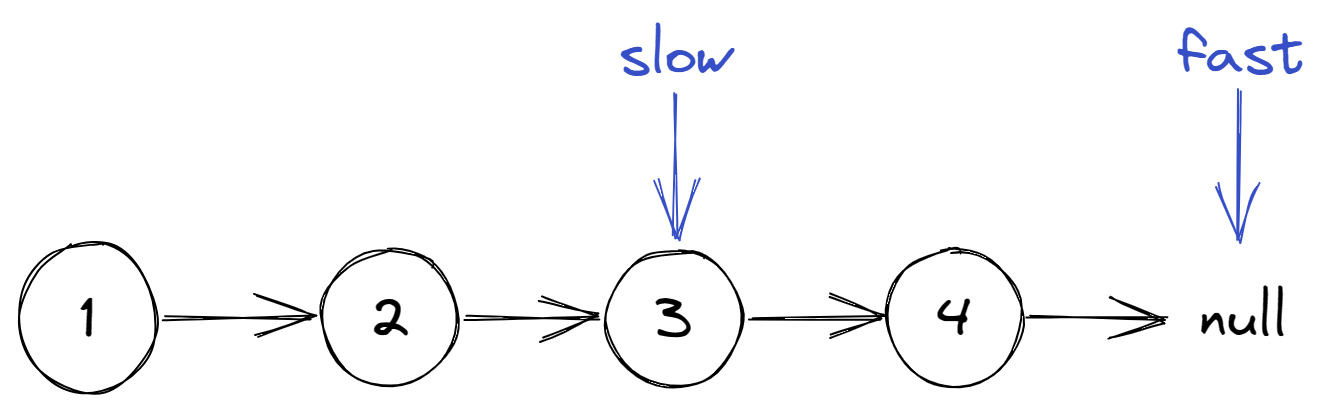
代码：

ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow == fast) {
        return null;
    }
}
return slow;

2. 是否是环形链表

算法：

1. 定义两个指针 slow 和 fast 指向 head ；
2. slow 每次向后走一步，fast 每次向后走两步；
3. 直到 fast 和 slow 指向相同的节点，则表明链表中存在环形链路。如果不存在环形链路，则 fast 会先到达终点。

说明：

为什么说 fast 和 slow 指向相同的节点就表明链表中存在环形链路呢？

如果链表中有环路，则慢指针 slow 一定会进入环内（此时快指针 fast 也已经进入了环内）。在环内快指针 fast 相对于慢指针 slow 的相对速度为 1 ，继续走下去快指针一定会追上慢指针。

代码：

ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow == fast) {
        return true;
    }
}
return false;

3. 查找环形链表的入口节点

算法：

1. 定义两个游标 slow 和 fast 指向 head ；
2. slow 每次向后走一步，fast 每次向后走两步；
3. 直到 fast 和 slow 指向相同的节点；
4. slow 继续单步向下走，同时 head 也单步向下走（注意这里是 head 不是 fast ）；
5. 直到两个指针（head 和 slow）相遇，这个相遇的节点就是环形链表的入口节点。

说明：

前面 3 步和 2. 是否是环形链表 的算法一样，比较难理解的是最后两步。

slow 和 fast 相遇时的情景如下：

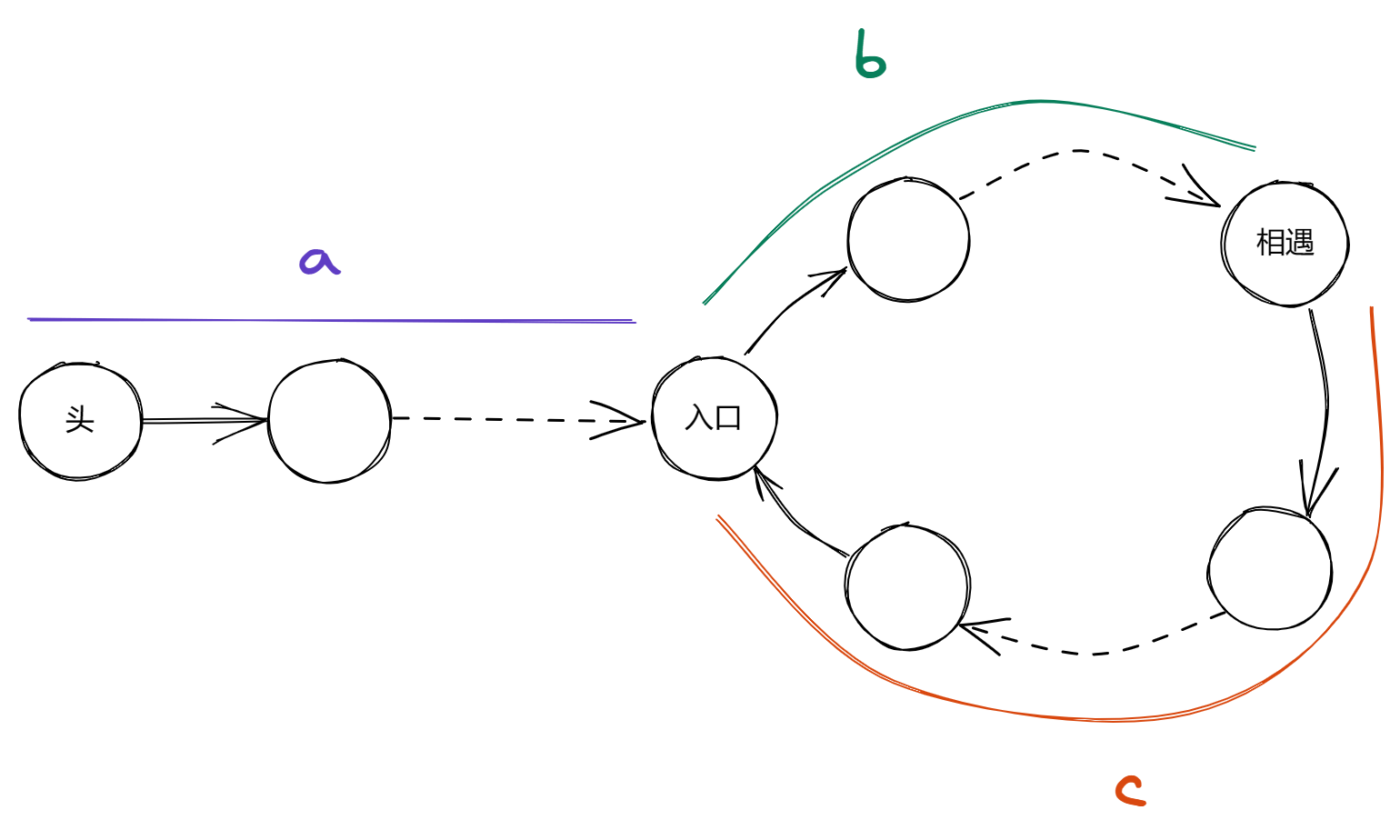
假设：

• head 到 入口 的步长 = $a$
• 入口 到 相遇点 的步长 = $b$
• 相遇点 到 入口 的步长 = $c$
• 快指针 fast 在环中重复移动的次数 = $k$

  注意： $k>0$ ，原因在于 fast 由于走的较快，肯定是先入环，而想要和 slow 相遇最快是在循环一次后恰好在 入口 相遇。

则可知：

• 环长 = $b+c$
• 慢指针 slow 移动距离 = $a+b$

  慢指针 slow 移动距离为什么是 $a+b$ 而不是 $a+b+n(b+c)$ （$n$ 为慢指针在环中绕圈的次数）。

  原因在于慢指针到达入口后，不管快指针位于环中何处，总能在

  • 最少 $0$ 步（即，慢指针到达入口时，刚好快指针也到达入口），
  • 最多 $b+c-1$ 步（即，慢指针到达入口时，快指针在慢指针的下一个节点）

  追上慢指针，也就是不满一圈，所以 $n$ 肯定为 $0$ 。

• 快指针 fast 移动距离 = $a+b+k(b+c)$

由于快指针移动距离是慢指针的两倍，则可得如下等式：

• $2(a+b)=a+b+k(b+c))$
• → $2(a+b)=a+b+b+c+(k-1)(b+c))$
• → $a-c=(k-1)(b+c))$

slow 和 fast 相遇时如图所示：

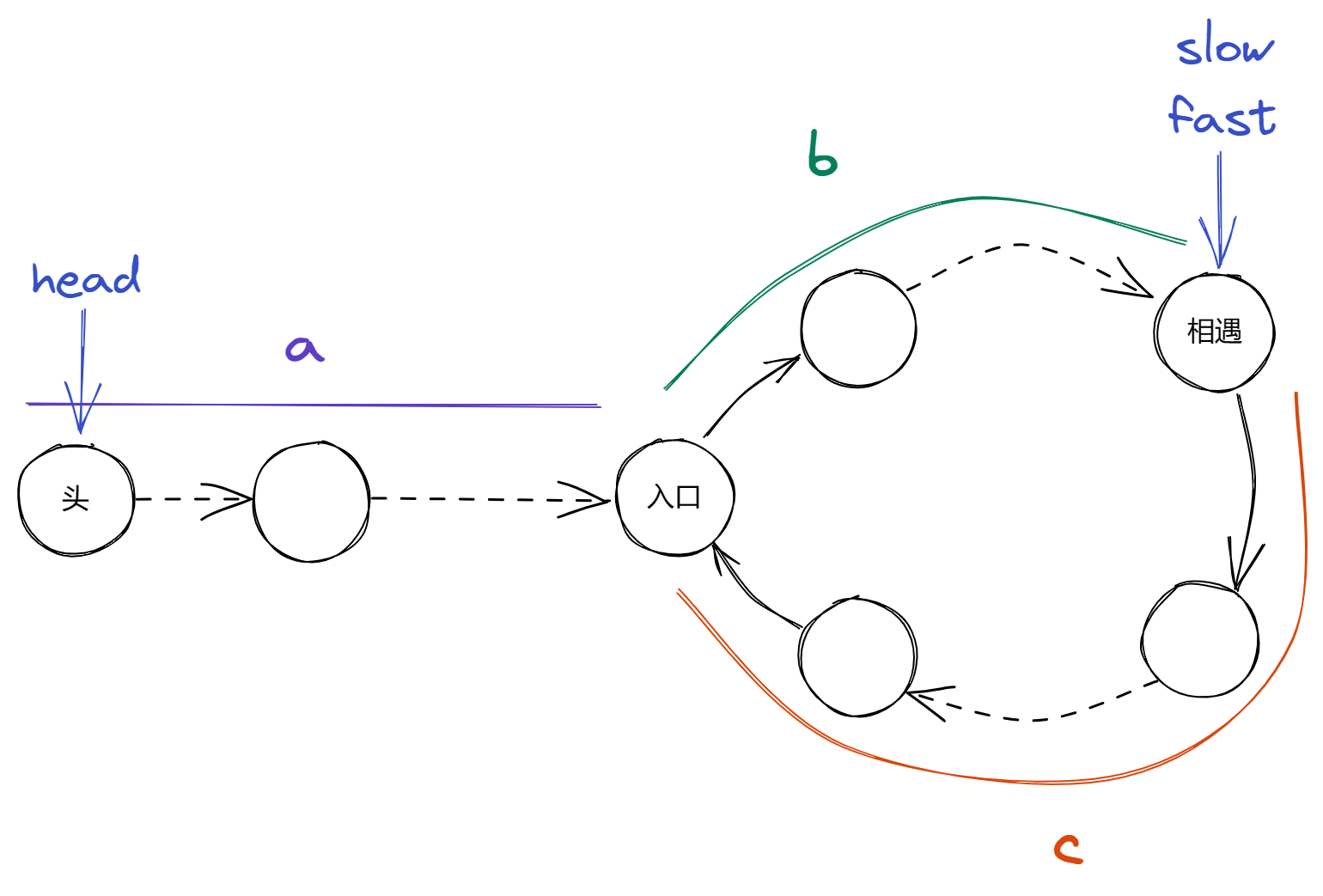
上述公式变换最后一步的结果意味着 head 若向后移动了 $c$ 步之后，此时 head 离 入口 的步长为 $(k-1)(b+c)$ （即 $(k-1)$ 倍的环长（由于 $k>0$，这个步长最小值为 $0$ ，也就是说在移动 $c$ 步之后，head 最多刚刚入环，不可能移动到 入口 之后的节点））。
若 slow 同样向后移动了 $c$ 步，则 slow 会位于环形的 入口 。

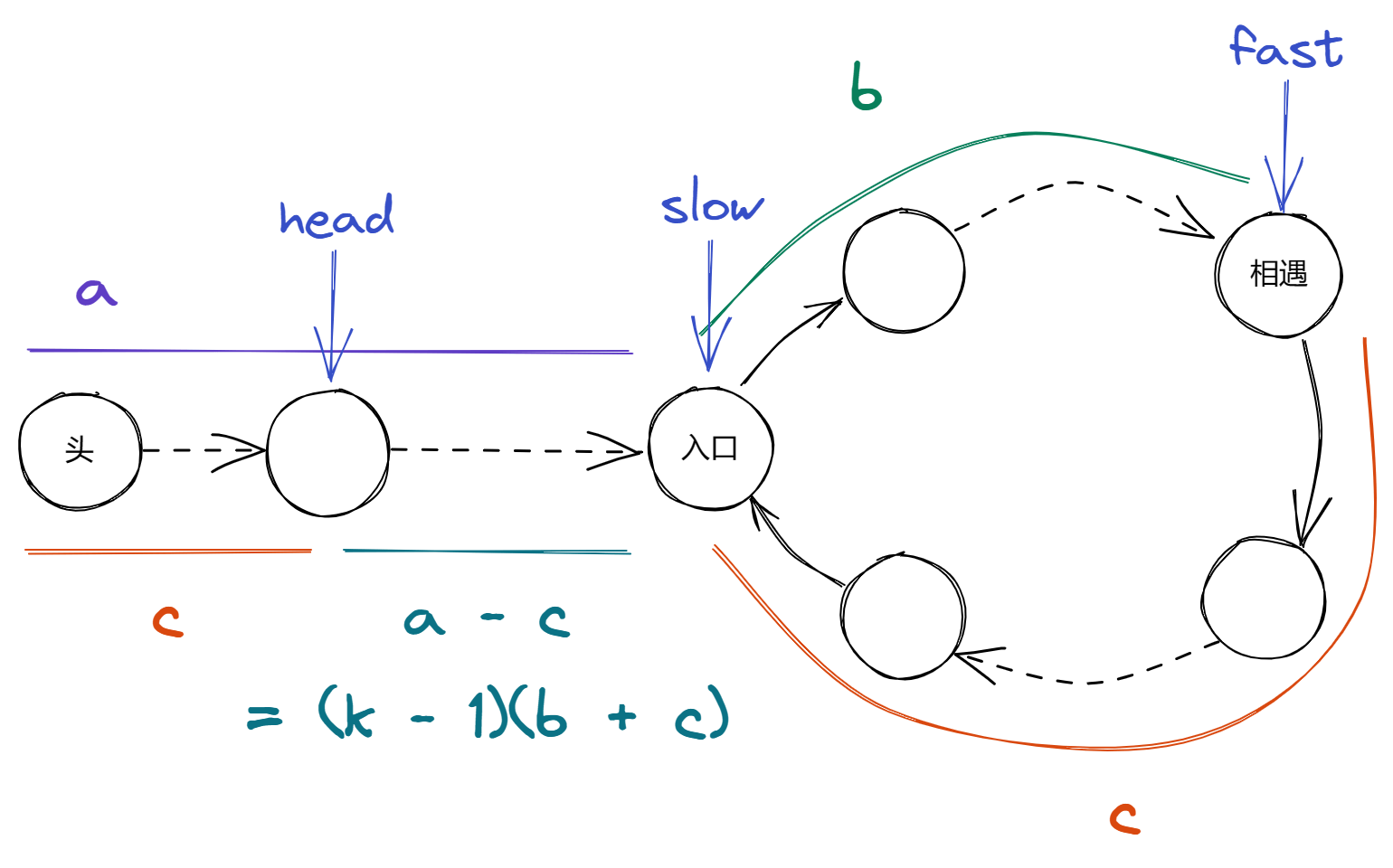
之后 head 继续向后移动 $a$ 路径的剩余部分（即 $a-c$ ）以到达 入口 ，则相当于移动了 $(k-1)(b+c)$ 。
若 slow 同样向后移动了 $(k-1)(b+c)$ 步，由于步数是环长的倍数，则 slow 也必然会位于 入口 。
此时两者就会在 入口 处相遇。

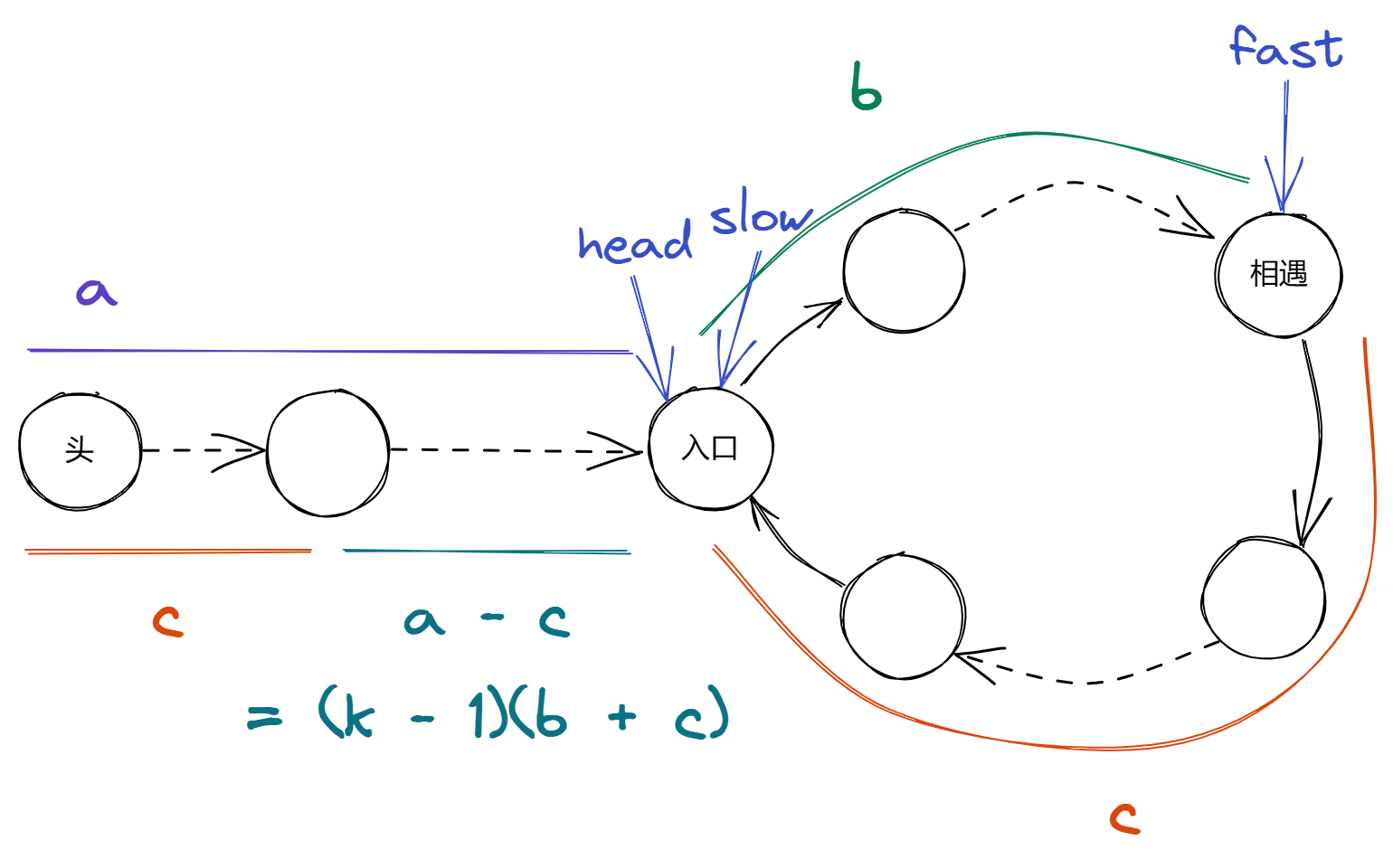
总的来说就是，在 slow 和 fast 相遇之后，若 head 和 slow（或 fast ）同步单步向后移动，则必然会在移动了 $a$ 步之后于 入口 处第一次相遇（代码中不需要关心 $a$ 的值为多少，只需要移动到两者相遇为止）。

代码：

ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow == fast) {
        while (head != slow) {
            slow = slow.next;
            head = head.next;
        }
        return slow;
    }
}
return null;