TAOCP 1.1 算法

看一本书上的介绍知道了这本书，看价格太贵就只买了第一卷。买来翻了几页感觉很庆幸，幸亏自己只买了第一卷。第一章的第一节都看了好久，完了还不知道自己理解的对不对。

这里记录下书中的主要内容及比较难理解的地方，作为笔记。

1.1 算法

算法是计算机程序设计的基本概念。

algorithm 这个词更古老的词形是 algorism ，它表示用阿拉伯数字进行的算数运算。在中世纪，珠算人员用算盘进行计算，而数算人员（ algorist ）则依据十进制计算规则用阿拉伯数字做计算。algorism 这个词的真正来源是波斯知名教科书作者的名字 Abū ʿAbd Allāh Muhammad ibn Mūsā al-Khwārizmī （中文也译作 花拉子米）。他关于印度和阿拉伯数学的著作被译作拉丁文，书名是《印度计算法》（ Algoritmi de numero Indorum ）。algoritmi 是其名字的拉丁文译名，后来演变成 algorithm （算法）一词。

1.1E 欧几里得算法

1.1E：表示第 1 章第 1 节的算法 E。

欧几里得算法：给定两个正整数 $m$ 和 $n$ ，求它们的 最大公因数 ，即同时整除 $m$ 和 $n$ 的最大正整数。

步骤

E1. [ 求余数。 ] 用 $n$ 除 $m$ ，令 $r$ 为余数。（我们将有 $0 \le r < n$ 。）
E2. [ 余数为 $0$ ？ ] 如果 $r = 0$ ，算法终止。 $n$ 是答案。
E3. [ 减少。 ] 置 $m \leftarrow n, n \leftarrow r$，然后返回步骤 E1。 ▋

本书中描述算法的格式都是这个样子的。应该还是很直观的，就不多做解释了。

如果 $m < n$ ，则首次执行时 $r$ 的值等于 $m$ ，再次执行 E1 相当于 $m$ 和 $n$ 做了交换，此时可以增加如下步骤 E0 以减少繁琐的交换。

E0. [ 保证 $m \ge n$ 。 ] 如果 $m < n$ ，交换 $m \leftarrow n$ 。

我写的 Java 版代码：

这里没有使用变量的交换，而是使用递归实现了类似的效果。不知道算不算是节后习题 3 的答案。

public class EuclidAlgorithms {
    public static void main(String[] args) {
        int r = getGCD(119, 544);
        System.out.println("119 和 544 的最大公因数是 " + r);
    }

    public static int getGCD(int m, int n) {
        if (m < n) {
            return getGCD(n, m);
        }
        int r = m % n;
        if (r == 0) {
            return n;
        }
        return getGCD(n, r);
    }
}

5 个特征

一个算法不仅仅是一组数量有限的规则，给出求解特定一类问题的一系列操作步骤，除此之外，它还具备如下 5 个重要特征。

有限性（有穷性）。算法必须在执行有限步之后终止。
确定性。算法的每一步都必须精确定义，对于每种情况要执行的操作必须给出严格而无歧义的说明。用计算机语言表示的计算方法称为程序（ program ）。
输入。一个算法具有 0 个或者多个输入（ input ）：算法开始前赋给它的初始量，或者在算法执行中动态赋给它的量。这样的输入取自特定的对象集合。
输出。一个算法具有 1 个或者多个输出（ output ）：与输入有着某种指定关系的量。
可行性（有效性）。通常还要求算法在下述意义下是可行的：它的所有操作必须足够基本，原则上人们可以用笔和纸在有限时间内准确地执行。

我们应当指出，有限性的要求太低了，不足以满足实际应用的需求。一个有用的算法的步骤数不仅应当有限，而且应当非常有限，大小合理。

在实践中，我们不仅需要各种算法，而且还要求这些算法在广义美学意义下是好的。好算法的一个标准是算法执行时间，这可以用每一步执行的次数来表达。

算法分析（algorithmic analysis）：给定一个算法，我们要确定它的性能特征。

欧几里得算法的平均执行次数为 $(12(\ln{2})/\pi^2)\ln{n}$ ，即与 $n$ 的 自然对数 成正比。

算法分析的一般思想是，取某个特定的算法，确定它的定量特性。算法理论则完全属于另一主题，它主要研究对于计算特定量是否存在可行算法。

集合论

在本节最后，简要介绍一种方法，把数学的集合论作为算法概念的坚实基础。

我们把一种计算方法形式地定义为一个四元组 $(Q, I, \Omega, f)$ ，其中

$Q$ 是包含子集 $I$ 和 $\Omega$ 的集合。
这个应该是说 $Q \supseteq I \cup \Omega$ 。
$f$ 是从 $Q$ 映射到自身的函数。
关于这一点不知道我理解的对不对。
我的理解是： $f$ 是一个函数，它的入参是集合 $Q$ 中的一个元素，它的返回值也是集合 $Q$ 中的一个元素。
也就是说 $Q = I \cup \Omega$
$\Omega$ 在 $f$ 下应保持点点不动；也就是说，对于 $\Omega$ 中的所有元素 $q$ ，$f(q)$ 应当等于 $q$ 。
我看到这里的时候理解错了，导致后面一段迷惑了好久。
这里的 $f(q)$ 应当等于 $q$ 只是对于 $\Omega$ 中的任意元素，而不是 $I$ 中的任意元素。也就是说 $\Omega$ 是 $I$ 的一个子集（ $\Omega \subseteq I$ ），而这个子集中的任意元素满足 $f(q) = q$ 。

四个量 $Q, I, \Omega, f$ 分别用来表示计算状态，输入、输出和计算规则。

计算状态 $Q$ 使用我上面递归的例子貌似比较容易理解。这个状态集合 $Q$ 中的元素就相当于递归调用过程中不是最终返回结果的那次调用时的入参，是计算中间过程的状态，因为本身就是入参，所以同时也属于入参集合 $I$ 。

集合 $I$ 中的每个输入 $x$ 定义一个 计算序列 $x_0,x_1,x_2,…$ 如下：

$$\tag{1} x_0 = x ~~ 和 ~~ x_{k+1} = f(x_k) ~~ 对于 ~~ k \ge 0$$

如果 $k$ 是使 $x_k$ 在 $\Omega$ 中的最小整数，就说计算序列在 $k$ 步内终止，此时就说从 $x$ 产生输出 $x_k$ 。（请注意，如果 $x_k$ 在 $\Omega$ 中，那么 $x_{k+1}$ 也在 $\Omega$ 中，因为此时 $x_{k+1} = x_k$ 。）某些计算序列可能永远不会终止。对于 $I$ 中的所有 $x$ 都能在有限步内终止的计算方法就是算法。

以算法 E 为例，它可以用这些术语形式化地表述如下：

令 $Q$ 为所有单元素（ $n$ ）、所有有序数偶（序偶）$(m,n)$ 以及所有四元组 $(m,n,r,1)$,$(m,n,r,2)$,$(m,n,p,3)$ 的集合，其中 $m,n,p$ 是正整数，$r$ 是非负整数。
令 $I$ 为所有有序数偶 $(m,n)$ 组成的 $Q$ 的子集，$\Omega$ 为所有单元素（ $n$ ）组成的 $Q$ 的子集。 $f$ 定义为：

$$\tag{2}
\begin{equation}
\begin{split}
f((m,n)) &= (m,n,0,1); ~~~~~~~~ f((n)) = (n); \
f((m,n,0,1)) &= (m,n，用n除m的余数，2);\
f((m,n,r,2)) &= (n) ~~ 如果 ~~ r = 0, ~~ (m,n,r,3) ~~ 其他情形;\
f((m,n,p,3)) &= (n,p,p,1)。
\end{split}
\end{equation}
$$

这种表示法同算法 E 之间的对应是显而易见的。

这里不包含 E0。

算法概念的这种表达方式，不再涉及前面提到的可行性的限制。例如， $Q$ 可以表示无法手工计算的无穷序列，$f$ 可以包含凡人有时无法执行的操作。如果我们想要限制算法的概念，使其只包含基本的操作，那么我们可以限制 $Q,I,\Omega,f$ ，例如设置如下的约束条件：

令 $A$ 为字母的有限集，
$A^*$ 为 $A$ 上所有字符串的集合（所有有序序列 $x_1x_2…x_n$ 的集合，其中 $n \ge 0$ ， $x_j$ （ $1 \le j \le n$ ）是 $A$ 中的元素）。

这步的思路是对计算状态编码，以便用 $A^*$ 的字符串表示计算状态。

现在令

$N$ 为一个非负整数，
$Q$ 为所有 $(\sigma,j)$ 的集合，其中 $\sigma$ 是 $A^*$ 中的元素，$j$ 是一个整数，$0 \le j \le N$ ；
$I$ 为取 $j = 0$ 时 $Q$ 的子集，
$\Omega$ 为取 $j = N$ 时 $Q$ 的子集。

如果 $\theta$ 和 $\sigma$ 是 $A^*$ 中的字符串，那么当 $\sigma$ 对于字符串 $\alpha$ 和 $\omega$ 具有 $\alpha\theta\omega$ 的行驶时，我们就说 $\theta$ 出现在 $\sigma$ 中。

最后，令 $f$ 为下述类型的函数，其中 $\theta_j$ 和 $\phi_j$ 是字符串，$a_j$ 和 $b_j$（ $0 \le j < N$ ）是整数：

$$\tag{3}
\begin{equation}
\begin{split}
f((\sigma,j)) &= (\sigma,a_j) ~~~~~~~~~~~ 如果 \theta_j 不出现在 \sigma 中;\
f((\sigma,j)) &= (\alpha\phi_j\omega,b_j) ~~~~~ 如果 \alpha 是满足 \alpha\theta_j\omega 的最短字符串;\
f((\sigma,N)) &= (\sigma,N).
\end{split}
\end{equation}
$$

这类计算方法的每一步显然是可行的。而且经验表明，这种模式匹配规则也足以胜任任何可以手工计算的工作。还有很多方法可以表述可行计算方法的概念（例如利用图灵机），它们在本质上是等价的。

上面这一段关于可行性限制的说明，完全没看懂。🥲

习题

[10] 正文中展示了可以利用替换记号，通过置 $t \leftarrow m$，$m \leftarrow n$，$n \leftarrow t$，交换变量 $m$ 和 $n$ 的值。请说明可以通过一连串替换，把四个变量 $(a,b,c,d)$ 重新排列成 $(b,c,d,a)$ 。换句话说，$a$ 的新值是 $b$ 的初始值，以此类推。试用最少的替换次数实现。
1. $t \leftarrow a$
2. $a \leftarrow b$
3. $b \leftarrow c$
4. $c \leftarrow d$
5. $d \leftarrow t$
答案：$t \leftarrow a$, $a \leftarrow b$, $b \leftarrow c$, $c \leftarrow d$, $d \leftarrow t$
[15] 证明从步骤 E1 第二次执行起，每次该步开始时，$m$ 必然大于 $n$ （第一次执行时可能不满足）。
- 在 E2 中，$r$ 是 $n$ 除 $m$ 的余数，此时必然满足 $r < n$ 。
- 执行到 E3 时，由于 $m \leftarrow n$，$n \leftarrow r$ ，所以上一步的 $r < n$ 到这一步就变成了 $n < m$ 。
- $\therefore$ 再次执行到 E1 时必然满足 $n < m$ 。
答案：在第一次执行步骤 E1 后，变量 $m$ 和 $n$ 的值分别是 $n$ 和 $r$ 原来的值，且 $n > r$ 。
[20] （为了提高效率）修改算法 E，使其避免出现 $m \leftarrow n$ 之类的平凡（频繁？）替换操作。按照算法 E 的风格写出这个新算法，将其称为算法 F。
- F1. [ 求余数。 ] 用 $n$ 除 $m$ ，令 $m$ 为余数。
- F2. [ 余数为 0？ ] 如果 $m = 0$ ，算法终止。$n$ 是答案。
- F3. [ 求余数。 ] 用 $m$ 除 $n$ ，令 $n$ 为余数。
- F4. [ 余数为 0？ ] 如果 $n = 0$ ，算法终止。$m$ 是答案。
- F5. [ 重复。 ] 返回步骤 F1。
更算法 E 类似也可以添加一个 $m \ge n$ 的判断，避免一次多余的取余运算。
- F0. [ 保证 $m \ge n$ 。 ] 如果 $m < n$，执行步骤 F3。
对比答案，比较严重的错误是缺少算法结束的符号 ▋ 。
答案：
- F1. [ 求 $m/n$ 的余数。 ] 用 $n$ 除 $m$ ，令 $m$ 为余数。
- F2. [ 余数是否为 0？ ] 如果 $m = 0$ ，算法终止。$n$ 是答案。
- F3. [ 求 $n/m$ 的余数。 ] 用 $m$ 除 $n$ ，令 $n$ 为余数。
- F4. [ 余数是否为 0？ ] 如果 $n = 0$ ，算法终止。$m$ 是答案；返回步骤 F1。 ▋
[16] 2166 与 6099 的最大公因数是多少？
2166 和 6099 的最大公因数是 57
答案：57
[12] 说明“阅读本套数的步骤”其实不是一个真正的算法，因为在算法的五个特征中，它至少缺少三个！另外请指出它与算法 E 在格式上的差异。
“阅读本套数的步骤” 是本书开头介绍的一段阅读方法，其流程图如下：
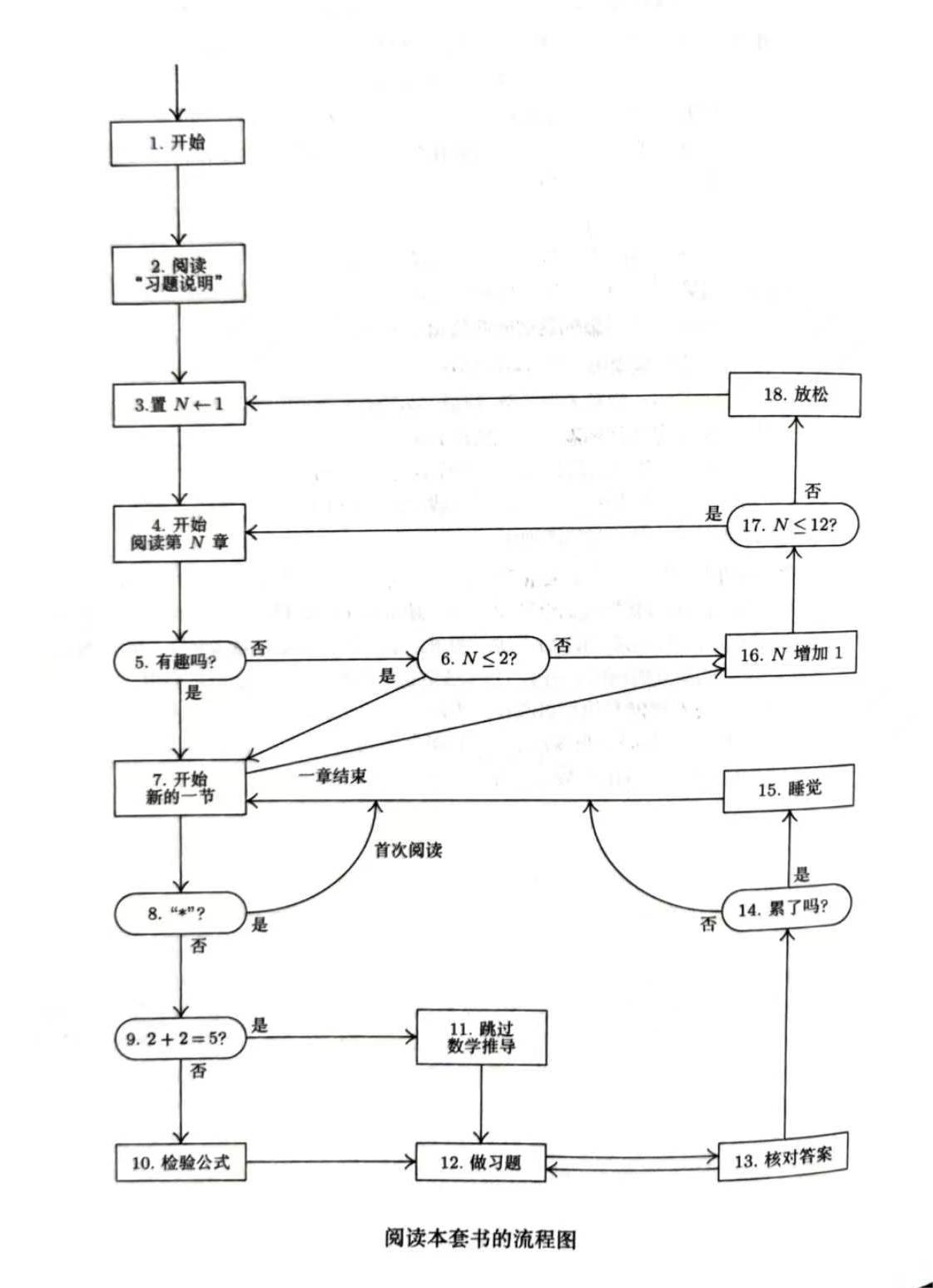
算法的五个特征：有限性（有穷性）、确定性、输入、输出和可行性（有效性）。
~~这个流程图个人认为不满足如下三个特征：~~
- ~~有限性（有穷性）：由于在 $N > 12$ 时会 $N \leftarrow 1$，所以这个步骤不会结束，不满足有限性。~~
- ~~输入：这些步骤没有输入~~
- ~~输出：这些步骤也没有输出。~~
答案：不满足有限性、确定性和可行性，可能没有输出。就格式而言，在操作步号码之前没有字母，未出现概述性短语，而且没有“▋” 。
[20] 当 $n = 5$ 时，执行算法 E 步骤 E1 的平均次数 $T_5$ 是多少？
2.6？：首先 $m$ 有接近 100% 的几率大于 $n$ 的值 5，所以可当作 E1 肯定会执行一步，并且其中有 $\frac 1 5$ 的几率余数为 0。之后 $m$ 的值将小于 $n$ ，此时有 4 种情况：
- 4:2 步
- 3:3 步
- 2:2 步
- 1:1 步
最终结果为：$0.2 + 0.8 \times (3 + 4 + 3 + 2) \div 4 = 2.6$
答案：用 $n = 5$ 和 $m = 1,2,3,4,5$ 实验算法 E，步骤 E1 执行的次数分别为 2,3,4,3,1，所以步骤 E1 执行的平均次数是 $2.6 = T_5$ 。
答案倒是一样，不过我的解题思路和答案差的有点多。
[M21] $m$ 已知，$n$ 在所有正整数范围内取值，令 $U_m$ 为算法 E 中步骤 E1 执行的平均次数。说明 $U_m$ 具有合理定义。$U_m$ 与 $T_m$ 有关系吗？
M 难度的连题目都看不懂~~
答案：除了数目有限的特例以外，$n > m$ 总成立，当 $n < m$ 时，算法 E 的第 1 次代仅仅交换这两个数，所以 $U_m = T_m + 1$. 例如 $m = 5$, $n = 1,2,…$, 1,2,3,2,1,3,4,5,4,2,3,4,5,4,2,… 的平均次数是 3.6 .
[M25] 通过指定式 $(3)$ 中 $\theta_j$，$\phi_j$，$a_j$，$b_j$，给出计算正整数 $m$ 和 $n$ 的最大公因数的“可行的”形式算法。令输入由字符串 $a^mbn$ 表示，也就是在 $m$ 个 $a$ 后连着 $n$ 个 $b$ 。你的解法应当力求尽可能简单。
[ 提示： 利用算法 E，把步骤 E1 中的除法改为置 $r \leftarrow |m - n|，n \leftarrow min(m,n).$ ]
本来书中关于这段的内容就没看懂，这里的题目也没看懂。
答案也没看懂。
答案：令 $A = {a,b,c}$，$N = 5$，算法结束时得到字符串 $a^{gcd(m,n)}$。
$$
\begin{matrix}
j & \theta_j & \phi_j & b_j & a_j \
0 & ab & (空) & 1 & 2 & 消除一个a和一个~~b，或者转到~~2。\
1 & (空) & c & 0 & 0 & 在最左端加~~c，转回~~0。\
2 & a & b & 2 & 3 & 把所有a变成b。\
3 & c & a & 3 & 4 & 把所有c变成a。\
4 & b & b & 0 & 5 & 如果还有~b，重复。
\end{matrix}
$$
每次迭代要么减少 $m$，要么保持 $m$ 不变并减少 $n$ 。
[M30] 假定 $C_1 = (Q_1,I_1,\Omega_1,f_1)$ 和 $C_2 = (Q_2,I_2,\Omega_2,f_2)$ 是两个计算方法。例如，$C_1$ 可以代表式 $(2)$ 中的算法 E，不过要限制 $m$ 和 $n$ 的大小；而 $C_2$ 可以代表算法 E 的一个计算机程序实现。（因此 $Q_2$ 可以是计算机所有状态的集合，也就是计算机内存和寄存器所有可能的配置；$f_2$ 可以是计算机单步操作的定义；$I_2$ 可以是初始状态的集合，包括确定最大公因数的相应程序以及 $m$ 和 $n$ 的值。）
试就“$C_2$ 是 $C_1$ 的一个表示”或者“$C_2$ 模拟 $C_1$”的概念，给出集合论定义。直观上，这意味着 $C_1$ 的任何计算序列都由 $C_2$ 模拟实现，不过 $C_2$ 可能要用更多的计算步骤，保留更多的状态信息。（因此，我们得以严格解释“程序 $X$ 是算法 $Y$ 的一个实现”这一陈述。）
这个答案太长了，自己也完全看不懂，就不整理出来了，有兴趣的还是直接看书吧。

两段关于 JavaScript 块级作用域的代码解析

TAOCP 1.1 算法

TAOCP 1.1 算法 link

1.1 算法 link

1.1E 欧几里得算法 link

5 个特征 link

集合论 link

习题 link

TAOCP 1.1 算法

1.1 算法

1.1E 欧几里得算法

5 个特征

集合论

习题