算法图解 - 广度优先搜索

最短路径问题 (shortest-path problem)

  • 解决最短路径问题的算法被称为广度优先搜索

图

  • 图模拟一组连接

  • 图由 节点 (node) 和 边 (edge) 组成

  • 一个节点可能于众多节点直接连接，这些节点被称为 邻居

  • 分为有向图 (directed graph) 和无向图 (undirected graph)

广度优先搜索

  • 广度优先搜索是一种用于图的查找算法，可帮助回答两类问题

    1. 从节点 A 出发，有前往节点 B 的路径吗？

    2. 从节点 A 出发，前往节点 B 的哪条路径最短？

队列

  • 只有两种操作

    • 入队

    • 出队

  • 是一种先进先出 (First In First Out, FIFO) 的数据结构

实现图

  • 使用散列表表示图的关系

    • 散列表的 key 表示节点

    • 散列表的 value 表示该节点的边

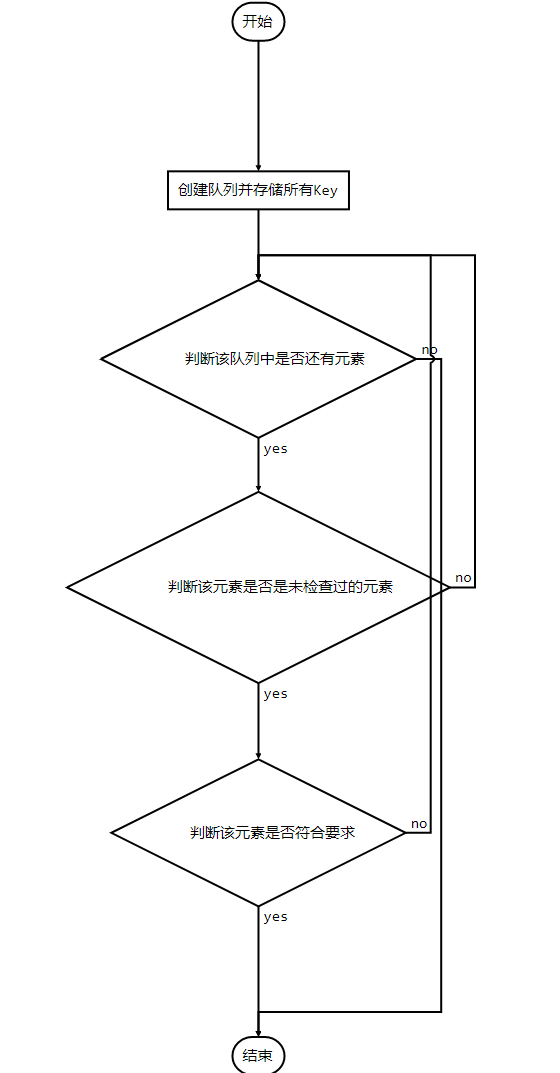
  • 实现算法

    1. 创建一个队列，存储所有的 key,

    2. 判断队列是否为空

      • 为空，则处理结束

      • 不为空，则处理继续

    3. 从队列中弹出一个元素

    4. 判断是否检查过该元素

      • 已检查过，则跳转到处理 2 继续执行

      • 未检查过，则处理继续

    5. 判断该元素符不符合要求

      • 符合，则处理结束

      • 不符合则跳转到处理 2 继续执行

运行时间

  • $O(人数 + 边数)$，通常写作

    $$O(V + E)$$

    其中 V 为顶点 (vertice) 数，E 为边数